Franco Colombo

Home Sicurezza Volo Antartide Curriculum Links

L’analisi spettrale dei dati climatici

Cap. Franco COLOMBO

Capo Sezione Meteo

41° Stormo – Sigonella

Abstract: The complexity of climate variabilty on all time scales requires the use of several refined tools to unravel its primary dynamics from observations. Indeed, ideas from the theory of dynamical system have provided new ways of interpreting the information contained in climatic time series.

We review the properties of several modern time series analysis methods and their respective advantages and limitations, illustrated by numerical experiments on syntetic time series, and on a real time serie (Catania Fontanarossa temperatures recorded during 1951-1990).

Introduzione: La complessità della variabilità del clima a tutte le scale di tempo, richiede l’uso di raffinati strumenti fisici e matematici, per rilevare la sua dinamica principale, a partire dalle osservazioni dei dati. L’analisi delle serie temporali è stata uno degli strumenti chiave nell’interpretazione della dinamica del clima, sin da quando è iniziata la raccolta e la catalogazione dei vari parametri meteorologici. La variabilità del clima, si verifica a tutte le scale temporali, con cicli che vanno dal diurno, all’annuale, al geologico, all’astronomico ecc.. ecc.

Le analisi delle serie temporali, hanno mostrato come le variazioni climatiche appaiano estremamente irregolari nel dominio spazio-temporale. Quest’ultima caratteristica le rende di conseguenza difficili da prevedere, a meno che non vengano utilizzate tecniche matematiche particolari. L’analisi spettrale delle serie temporali, rappresenta un ponte tra la descrizione del fenomeno, desunto dalle osservazioni, e lo studio delle origini della dinamica del clima. Per lo studio di questi collegamenti si è fatto uso della teoria dei sistemi dinamici, attraverso cui è possibile comprendere il modo in cui le principali sorgenti delle variazioni climatiche intervengono per determinare la variabilità del clima stesso. Nel presente articolo, verranno descritte diverse tecniche di analisi, e si valuteranno le differenze fra i risultati con esse ottenibili, applicandole sia a una serie temporale sintetica costruita in modo da simulare l’andamento temporale della radiazione solare incidente al top dell’atmosfera su una scala di tempi dell’ordine delle migliaia di anni, sia alla serie di temperature osservate nel periodo 1951-1990, presso la stazione meteorologica di Catania-Fontanarossa.

Metodi di analisi spettrale

Sia i processi deterministici che quelli stocastici possono, in linea di principio, essere caratterizzati per mezzo di una funzione della frequenza (anziché del tempo) chiamata spettro di potenza. Così, per esempio, un movimento molto irregolare (es. il rumore), possiede uno spettro piatto, continuo e regolare, il che indica che tutte le frequenze in una banda di frequenze molto larga, sono eccitate da questo processo. D’altro canto, nel dominio della frequenza, un processo puramente periodico o quasi periodico, può essere generalmente caratterizzato da una singola linea o un insieme costituito da poche linee, aventi un’ampiezza notevolmente maggiore di tutte le linee spettrali successive. Fra questi due estremi, i processi non lineari deterministici, possono avere dei picchi spettrali sovrapposti ad un fondo continuo e regolare.

Il calcolo dello spettro di potenza di un processo casuale è essenzialmente un problema inverso mal posto (Thomson, 1982). Per esempio, il semplice calcolo della trasformata discreta di Fourier di una serie temporale casuale (con densità spettrale continua), darà una stima spettrale la cui varianza è uguale alla stima stessa. Di seguito vengono illustrati alcuni metodi per ridurre questa varianza, che vengono utilizzati per l’analisi spettrale di serie temporali climatiche.

Il metodo Blackman e Tukey o Fast Fourier

Il metodo Blackman-Tukey è il classico metodo per effettuare analisi spettrali. L'algoritmo calcola prima la autocorrelazione dei dati, quindi applica una finestra, e infine esegue una trasformata di Fourier per calcolare lo spettro. E' un metodo molto efficace, che sfortunatamente presenta caratteristiche spettrali spurie.

Il metodo Blackman-Tukey (Blackman e Tukey, 1958) dà una stima dello spettro di potenza che riduce la varianza delle stime spettrali di una dato segnale reale X ed attenua gli effetti di perdita dovuti alla finitezza della finestra in cui sono campionati i dati (Chatfield, 1984). Il punto di partenza di questo metodo è l’identità Wiener-Khintchine, la quale stabilisce che lo spettro di potenza _x= è uguale alla trasformata di Fourier della funzione di auto-correlazione ØX= (Jenkins e Watts, 1968). Ne deriva che lo spettro di potenza può essere approssimato da una versione discretizzata di questa identità, mediante i primi M + 1 coefficienti di auto-correlazione.

[1]

Questa operazione, spesso chiamata periodogramma, smussa lo spettro e riduce la varianza delle stime spettrali. In questa formula, la scelta di M è legata a un compromesso fra la risoluzione in frequenza ( grandi valori di M) e la varianza delle stime che è proporzionale a M/N, dove N è il numero di dati sperimentali.

Pertanto, una accettabile regola generale consiste nel prendere M più piccolo di N/5 o N/10, per evitare risultati spuri dovuti alle alte varianze delle stime. Inoltre, una finestra o taper è applicata ai dati, in modo da ridurre la perdita spettrale, per mezzo dello smorzamento dei lobi laterali della trasformata della funzione gradino. Tali finestre vengono scelte empiricamente come funzioni coseno modificate o funzioni cubiche ecc... (Chatfield, 1984).

I livelli di confidenza su un puro rumore rosso (con pendenza dello spettro ) si possono calcolare (Jenkins e Watts, 1968), ma la risoluzione spettrale è generalmente scarsa se il numero di dati sperimentali è basso.

Il metodo della Massima Entropia

Il metodo dell’Entropia Massima (MEM) è particolarmente potente per la stima delle linee di frequenza in serie temporali auto-regressive. Sono disponibili dettagli esaurienti in Burg (1967), Childers (1978) o Haykin (1983).

In breve, si inizia con una serie temporale stazionaria X di media zero, con M+1 coefficienti di auto-correlazione ŒØX(k), k = 0 ... M:X

ØX(k)= [2]

Lo scopo è quello di determinare la densità spettrale Px che corrisponde al processo più casuale o imprevedibile descritto dagli stessi coefficienti di autocorrelazione. In termini di teoria dell’informazione, questo costituisce la nozione di entropia massima: ecco quindi l’origine del nome del metodo.

L’imprevedibilità è misurata per un processo Gaussiano dalla entropia h:

h = 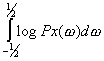[3]

Il funzionale [3] è massimizzato rispetto ai coefficienti di autocorrelazione ØX ottenuti dalla relazione di Wiener-Khintchin [1]. Questo problema di ottimizzazione viene risolto mediante M multiplicatori di Lagrange {a k }. Questi multiplicatori di Lagrange corrispondono ai coefficienti di una serie cronologica auto-regressiva (AR): X(t) i cui coefficienti di autocorrelazione sono ØX:

[4]

dove x è un rumore bianco residuo. Una stima della densità spettrale di potenza di Fourier Px di questo processo AR è data da

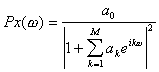[5]

dove a0 è la varianza del rumore x . Pertanto, la conoscenza dei coefficienti

{ ak }, k = 0 ... M fornisce direttamente una stima dello spettro di potenza di X. I coefficienti { ak } possono essere calcolati risolvendo un sistema di equazioni lineari (Pestiaux, 1984; Press et al., 1988), con una matrice di auto-correlazione simmetrica Teoplitz:

Ø0

Ø1

ØM

Ø0

ØM-1

. . .

ØM

ØM-1

Ø0

[6]

Una tecnica alternativa consiste nel prendere la matrice di auto-covarianza per le M coordinate selezionate (Martin, 1984). Questa matrice è definita positiva ma non è di tipo Toeplitz. Questa tecnica sembra essere meno sensibile alla fase del segnale ed introduce minori distorsioni in frequenza (Martin, 1984; Benoist, 1986).

Il metodo di massima entropia è molto efficiente per la rilevazione delle linee di frequenza per le serie cronologiche stazionarie. Se questa ipotesi non viene verificata, o se la serie cronologica non è quasi auto-regressiva, si possono ottenere risultati fuorvianti, che non è possibile rilevare se non analizzando le serie cronologiche con altre tecniche.

Inoltre, si rileva che il comportamento della stima spettrale dipende molto dalla scelta dell’ordine M di auto regressione: il numero di picchi nello spettro aumenta con M a prescindere dal contenuto della serie temporale. Ciò significa che risultati anomali possono apparire per elevati valori di M. Un limite superiore per M è generalmente considerato N/2. Sono stati proposti criteri empirici per la ottimizzazione del valore di M, basati sulla minimizzazione del residuo di una regressione col metodo dei minimi quadrati fra l’approssimazione autoregressiva dei dati e la serie temporale originaria.

Il metodo Multitaper

Il metodo Multitaper è relativamente nuovo. Esso offre diverse caratteristiche interessanti: una alta risoluzione e varianza delle stime che sono statisticamente indipendenti dalla potenza spettrale (oscillazioni piccole in ampiezza possono avere un livello di significatività alto). Alcune cautele sono sempre necessarie: il livello di confidenza statistica valutato per questo metodo, è spesso più ottimistico rispetto a quello dato per i metodi classici.

Lo scopo di questo metodo spettrale non parametrico (Thomson, 1982) è quello di calcolare un insieme di stime indipendenti e significative dello spettro di potenza, per ottenere una migliore e più affidabile stima di quanto non sia possibile con i metodi della singola finestra (Blackman-Tukey), in presenza di una serie cronologica finita. Un insieme di finestre rastremate ottimali è calcolato in modo che questa tecnica di stima spettrale sia meno euristica di quelle tradizionali (per es. Blackman e Tukey).

Il metodo multi-taper (MTM) di Thomson (1982) è stato applicato a vari campi della geofisica, compresa la scienza della Terra (Lindberg, 1986; Park et al., 1987), la geofisica (Lanzerotti et al., 1986), la climatologia sulle scale temporali interdecennali e secolari (Kuo et al., 1990; Ghil e Vautard, 1991; Mann et al., 1995) e la paleoclimatologia, su dati relativi agli anelli di accrescimento degli alberi (Thomson, 1990), dati ricavati da carote marine (Thomson, 1990; Berger et al., 1991; Park e Maasch, 1993) e dati ricavati da carote di ghiaccio (Yiou et al., 1991, 1994).

Supponiamo che {X(t)} sia una serie cronologica sinusoidale di frequenza angolare , per esempio, X(t) = per t = 0 ... N - 1. Allora sia { w(t), t = 0 ... N - 1} una finestra di lunghezza N e che {y(w)} sia la Trasformata di Fourier Discreta (DFT) del segnale finestrato {X(t)w (t)}:

[7]

dove è la frequenza angolare, con k = 0, 1, …. N-1.

Lo scopo primario della finestra rastremata è di minimizzare le perdite spettrali, ovvero di minimizzare il contributo energetico al di fuori di una determinata larghezza di banda ( - W, + W) del segnale finestrato con frequenza angolare , dove ½y(w)½2 è una stima della potenza del segnale. Pertanto, il segnale finestrato {X(t)w(t)} dovrebbe mantenere quanto più possibile della propria energia nell’intervallo ( - W, + W), relativamente alla potenza totale che copre l’intera banda (-p,p). Pertanto, si può scegliere una finestra {w(t)} tale da massimizzare il funzionale

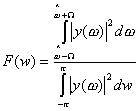[8]

Nel massimizzare F rispetto a {w(t)} sorge un classico problema Rayleigh-Ritz, le cui soluzioni sono date da un problema agli auto vettori con matrice Toeplitz (Thomson, 1982). Le finestre ottenute da questi auto vettori sono chiamate successioni sferoidali prolate discrete (Discrete Prolate Spheroidal Sequences DPSS) (Slepian, 1978). Per costruzione, esse sono ortogonali; quindi gli spettri associati forniscono stime indipendenti dello spettro reale. Se ordiniamo gli auto vettori mediante i loro corrispondenti auto valori

1 > l1 > ... lN > 0,

l’espressione 1 - lk dà la frazione dell’energia totale della k° finestra al di fuori dell’intervallo (- W, + W). È evidente che i primi K = [2N.W] auto vettori (laddove [.] significa parte intera) hanno le migliori proprietà spettrali, dato che le relative frazioni di perdita 1 - lk, k = 1 ... K sono molto vicine ad uno (Slepian, 1978). Pertanto, si devono prendere al massimo K = [2NW] finestre, per ottenere una stima spettrale efficiente. Slepian (1978), Thomson (1990) e Rögnvaldsson (1993) forniscono algoritmi efficienti per la computazione delle DPSS.

Di seguito, indicheremo con {y_k(w)} la Trasformata Discreta di Fourier del segnale finestrato {X(t)w_k(t)}.

Una volta calcolate la finestre, si può stimare lo spettro di potenza totale, facendo la media dei singoli spettri di ciascun segnale finestrato. Quindi, se definiamo Š_k( ) = ½Y_k( )½2 il k° auto spettro della serie temporale {X(t)}, la stima dello spettro totale ottenuta dalle prime K finestre è:

Š( )= Šk( ) [9]

La risoluzione è quindi ±W, che significa che le linee spettrali saranno rilevate mediante picchi o gobbe di larghezza 2W. Il vantaggio di questa stima multi taper è che il processo di media su diverse stime indipendenti Sk dello spettro reale, attenuano le irregolarità spurie e quindi riducono la varianza della stima. La varianza può essere ulteriormente ridotta e le barre di errore possono essere calcolate applicando le cosidette procedure «jack-knifing» alle K stime (Rögnvaldsson, 1993).

Lo scopo dell’analisi armonica è di determinare le linee spettrali di un segnale periodico o quasi periodico e le relative ampiezze. La trasformata di Fourier di un segnale periodico infinito fornisce una funzione del tipo di Dirac alla frequenza del segnale, cioè un picco di altezza infinita. Una stima spettrale semplice (dal metodo di entropia massima, o dalla trasformata di Fourier) fornisce informazioni indirette sull’ampiezza di un segnale ad una data frequenza, attraverso l’area sotto il picco, che è approssimativamente costante, anche se l’altezza del picco è proporzionale al numero di punti nella serie temporale, e tende ad infinito al crescere di questo numero. Quindi, lo scopo dell’analisi armonica è di definire un modo per avere un accesso diretto all’ampiezza di un’oscillazione periodica.

Presumiamo ora che il segnale {X(t)} sia la somma di una sinusoide con frequenza angolare ed ampiezza µ, e di un rumore {x(t)}, che è la somma di altre sinusoide e di rumore bianco. Si può scrivere

X(t) = + x(t)

[10]

Nel considerare le prime K DPSS , noi chiameremo{ Uk( )} la trasformata discreta di Fourier di {w_k(t)}.

Una regressione nel senso dei minimi quadrati nel dominio delle frequenze, fornisce una stima dell’ampiezza µ:

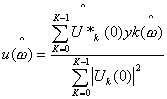[11]

dove l’asterisco indica coniugazione complessa. Una misura di affidabilità statistica può essere ottenuta mediante un test di Fisher. Questo test è approssimativamente basato sul rapporto fra la varianza “spiegata” dal modello [10], e la varianza residua. Se si espande la varianza del modello, si trova che è la somma di due termini:

[12]

[13]

che rispettivamente sono il contributo alla varianza “spiegato” e residuo.

La variabile casuale

[14]

segue una legge Fisher-Snedecor con 2 e 2K - 2 gradi di libertà se il segnale si comporta come Gaussiano. Si può interpretarne il valore presumendo che µ = 0, cioè una serie “bianca”, e provando a rigettare questa ipotesi con la più bassa probabilità di errore.

Con questo metodo si possono rilevare oscillazioni di piccola ampiezza in un serie cronologica relativamente breve, con un alto grado di significatività statistica, oppure scartare un picco di grande ampiezza se fallisce al test F, perchè il valore F non dipende in prima approssimazione dal valore di µ ( ). Questo significa in pratica che questo test è robusto nel caso di rumore bianco e dà ancora risultati ragionevolmente buoni con il rumore colorato, come quello presente in molte serie temporali climatiche. Mann e Lees (1996) hanno messo a punto test specifici per rumore rosso.

Una delle assunzioni principali di questa tecnica di analisi armonica è che il segnale deve fornire componenti periodiche separate. In caso contrario, uno spettro continuo (nel caso di rumore rosso o di un sistema caotico) sarà spezzato in linee spurie con frequenze arbitrarie e possibilmente con valori F alti. Questo è uno degli inconvenienti del metodo, che può essere parzialmente evitato se viene calcolato uno spettro grezzo di potenza e rilevate evidenze di linee spettrali; è molto importante anche variare il parametro larghezza di banda WN ed il numero di finestre, per assicurarsi della stabilità delle stime di frequenza e di ampiezza. WN = 4 viene generalmente presa come scelta WN iniziale, che implica K £ 7 finestre (Lindberg, 1986; Park et al., 1987). Successivamente la larghezza di banda può essere modificata in funzione della lunghezza delle serie temporali, e delle frequenze che devono essere investigate.

Analisi spettrale su dati sperimentali

Le serie temporali utilizzate per effettuare un confronto sui risultati prodotti dai diversi metodi di analisi sono di due tipi. Il primo consiste in una simulazione di una serie climatica che descrive la variabilità della radiazione media incidente al top dell’atmosfera, di una località posta ad una latitudine media dovuta alle componenti astronomiche di eccentricità, obliquità e precessione. Essa è stata realizzata sommando cinque sinusoidi, con periodi ed ampiezze tali da simulare i cicli astronomici di Milankovitch, le cui periodicità, ampiezze relative e relazioni di fase attuali, sono descritte nella tabella 1.

Il segnale risultante è stato sporcato con rumore con caratteristiche statistiche diverse e generalmente pessimistiche rispetto alla possibile variabilità climatica , al fine di valutare meglio le potenzialità di ogni singolo metodo li analisi.

Tabella1: coefficienti delle sinusoidi usate nella simulazione della serie

	Periodo (x 1000 anni)	Ampiezza	Fase (in gradi)	Frequenza (1/1000 anni)
Eccentricità	400	0.8	165	0.00250
	95	0.6	100	0.01053
Obliquità	41	6.3	72	0.02439
Precessione	23.7	18.5	122	0.04219
	22.5	16.2	287	0.04440

In pratica, ai segnali di base sono state sommate una componente di rumore di tipo gaussiano con standard deviation =10 e 2, ed una componente di rumore rosso correlato: ,

dove è un rumore bianco con standard deviation =5; è un coefficiente di correlazione uguale a 0.9:

, t= 1…….n

Il secondo tipo di test è stato effettuato su una serie di dati reali di temperatura, messi a disposizione dal Servizio Meteorologico dell’Aeronautica, relative al periodo 1951-1990, osservate presso la stazione meteorologica di Catania Fontanarossa. Il periodo di campionamento dei dati è di 3 ore.

Serie temporale sintetica

La serie sintetica è stata generata utilizzando il semplice algoritmo:

function z=p1(w,n)

s1=10;

s2=5;

g=0.9;

z=0;

m=size(w,1);

u=[1:n];

for k=1:m

x=w(k,2)*sin(2*pi*u/w(k,1)+w(k,3));

z=z+x;

end

q(1)=rand;

for l=2:n

q(l)=0.9*q(l-1)+randn*s2;

end

z=z+q+randn(1,n)*s1;

if nargout==0

plot(z)

clear z

end

dove w è la matrice contenente i parametri in tabella 1 e n il numero di valori della serie.

Nella figura 1 è descritto un andamento della serie per un periodo di 1000 Kyr., ottenuta con l’algoritmo appena descritto.

La successione di analisi eseguite sui dati sintetici, utilizzando come software il programma “MATLAB”, è stata così articolata:

· Analisi Fast Fourier sulla serie sintetica utilizzando un campione rispettivamente di 10000e 1000 punti, ed inserendo un rumore crescente con 2 e con 10 + rumore rosso (figg. da 2 a 5);

· Analisi Multi-Taper sulla serie sintetica utilizzando un campione rispettivamente di 10000 e 1000 punti, ed inserendo un rumore crescente come sopra, ed utilizzando un parametro N = 2 (figg. da 6 a 9);

· Analisi della Massima Entropia sulla serie sintetica utilizzando un campione rispettivamente di 10000 e 1000 punti, inserendo un rumore crescente come sopra, ed utilizzando una numero di coefficienti di autoregressione = 200 (figg. da 10 a 13).

L’analisi Fast Fourier eseguita sulla serie sintetica, si è mostrata molto efficace sulla serie sintetica restituendo sia le frequenze che le ampiezze del segnale in maniera soddisfacente se si eccettua un sottostima di circa il 30% dell’ampiezza del picco con periodo più breve. (Figg. 2, 3 , 4 e 5)

Il metodo Multi Taper ,rispetto alla Fast Fourier, non restituisce una singola frequenza, ma viene individuato un range di frequenze centrate intorno al valore ricercato; i rapporti di ampiezza sono sempre corretti, ed anche i valori assoluti non si discostano molto dalle ampiezze cercate. (Figg. 6, 7, 8 e 9)

Il metodo della Massima Entropia, è in grado di filtrare completamente il rumore evidenziando soltanto il segnale. E’ necessario scegliere bene il numero di coefficienti di autoregressione, tenendo conto soprattutto del segnale analizzato. (Figg. 10, 11, 12 e 13)

Nelle figure 14 e 15 seguenti vengono messi a confronto i tre grafici ottenuti dai rispettivi metodi di analisi, sulla serie contenente 10000 campioni e con il massimo rumore, presi in corrispondenza del picco con periodo 41 Kyr e dei picchi precessionali intorna a 20 Kyr.(Figg. 14 e 15).

Da notare come il Metodo della Massima Entropia sia in grado di eliminare i picchi spuri dal segnale, lasciando solamente i picchi ricercati.

Serie sperimentale

La serie temporale sperimentale scelta per effettuare il confronto sui risultati prodotti dai diversi metodi di analisi, è la serie storica delle temperature dell’aria osservate del periodo 1951 – 1990 presso la stazione meteorologica di Catania Fontanarossa. I dati sono stati estrapolati dai messaggi Synop. Le ore di osservazione sono quelle sinottiche, ovvero le 00, 03, 06, 09, 12, 15, 18, 21 U.T.C. per un totale di 8 osservazioni giornaliere. Il numero totale di osservazioni di cui è composta la serie è 116880 campioni. Sulla serie sono stati eseguiti i tradizionali test statistici i cui risultati sono riassunti nella tabella 2 .

Tabella 2

Media	17,2	Massima	45,0	Standard Deviation	6,9
Mediana	17,0	Minima	-4,0	Median absolute deviation	5,0
Moda	14,8	Range	49,0	Mean absolute deviation	5,7

La serie contiene un ciclo diurno legato al moto di rotazione terrestre, ed un ciclo annuale legato al moto di rivoluzione intorno al sole. Entrambi questi cicli dovrebbero essere individuati dalle analisi spettrali, ma la nostra attenzione è stata puntata sui cicli con periodo superiori all’anno, i quali potrebbero dare indicazioni sulle oscillazione legate a fattori interni alla terra.

Il primo tipo di analisi eseguito sulla serie completa è stata una Fast Fourier. Mediante questo questo metodo è stato determinato in maniera molto precisa il ciclo annuale con periodo 365.5 ed ampiezza 80 ed il ciclo diurno. (Figg. 16 e 17)

In vicinanza del picco annuale è presente un picco con ampiezza molto minore con periodo 182 giorni (periodo semestrale), giustificabile come armonica del picco principale.

Anche per il picco diurno individuato con frequenza = 0,125 ad ampiezza 42 sono state individuate armoniche con periodo 12 ore e 6 ore.

Questo metodo, applicato alla serie completa, non permette di distinguere periodi superiori ad un anno, in quanto non sono distinguibili dal rumore di fondo; tuttavia, analizzando il primo picco stabile con periodo superiore ad un anno, è emerso che questo ha un periodo pari a 420 giorni, ovvero molto prossimo al periodo dell’oscillazione di Chandler, uno dei moti terrestri causato dalla non perfetta coincidenza dell’asse di rotazione con l’asse di massimo momento di inerzia della Terra (Fig. 18)

I risultati ottenuti utilizzando il metodo Multi-Taper e della Massima entropia, sono messi a confronto nelle figure 19 e 20.

Il metodo della massima entropia è l’unico non in grado di rilevare il picco annuale e semestrale, mentre sono ben evidenti i picchi a periodo diurno e le relative armoniche. Il raffronto grafico tra i risultati ottenuti applicando i diversi metodi, evidenziano quanto sopra esposto.

Aumentando i coefficienti di autoregressione a 2000, l’analisi della massima entropia è in grado di individuare il picco con periodicità annuale.(Fig. 21)

Il passo successivo fatto nell’analizzare la serie e confrontare i vari metodi di analisi, è stato quello di eliminare la periodicità diurna, utilizzando i valori medi giornalieri, ottenuti come media delle otto osservazioni.

In questo caso, tutti i metodi riescono ad individuare le periodicità annuale e semestrale, mentre periodi più lunghi rimangono, se presenti, mascherati dal rumore.(Figg.22

Conclusioni

Nel presente articolo, sono stati presentati diversi metodi per l’analisi delle serie temporali. Ognuno di questi metodi ha evidenziato particolari caratteristici di tali serie (spettro di potenza, periodicità, stazionarietà ecc). Sono state descritte le tecniche per estrarre dal dato grezzo, informazioni importanti quali:

- stima dello spettro di potenza del segnale;

- calcolo delle linee di frequenza a delle ampiezze associate;

- separazione del trend, oscillazione e componenti di rumore.

Confrontando i risultati ottenuti utilizzando metodi diversi, si possono estrarre informazioni importanti sul sistema che genera i segnali fisici oggetto di studio. In particolare l’utilizzo di tecniche diverse permette di eliminare alcuni picchi spuri causati dal rumore, sempre presente nei segnali fisici.

Un problema molto limitante nello studio delle serie climatiche, è la loro relativa brevità, e questo rende alcune tecniche di analisi poco efficienti. Tuttavia si è visto come tecniche particolari, quali il Multi-taper siano in grado di dare buoni risultati anche in presenza di serie relativamente brevi. Quando invece la lunghezza della serie non rappresenta un problema, allora quasi tutte le tecniche hanno dato buoni risultati.

In conclusione, l’analisi delle serie temporali è diventata di grande importanza nello studio dei dati climatici, soprattutto grazie al notevole aumento delle osservazioni disponibili. Purtroppo, la complessità dei processi che originano il clima di una località, non permette di trarre delle conclusioni certe, avendo a disposizione soltanto i risultati di queste analisi.

Bibliografia

Bath M., 1974, “Spectral analysis in geophisics”, Elsevier, 563 pp.

Berger A.L., Mèlice J.L. and Hinnov L., 1991 “A strategy for frequency spectra of quaternary climate records”, Clim. Dyn. 5, pag. 227-240.

Benoist J.P., 1986, “Analyse Spectrale de Signaux Glaciologique: Etude des Glaces Sèdimentaires Deposèes à Dome C, Morphologie du Lit d’un Glacier”, Thèse d’Etat, USMT Grenoble, France.

Blackman R.B and Tukey J.W, 1958, “The Measurement of Power Spectra from the point of View of communication Engineering” , Dover, New York.

Blackman R.B and Tukey J.W, 1959, “The Measurement of Power Spectra”, Dover Publications, 190 pp.

Burg J.P., 1967, “Maximum entropy spectral analysis”, in 37^th Ann.Intern.Meeting. Soc. Explor. Geophis., Oklaoma City, OK.

Chatfield C, 1984, “The analysis of time series: An introduction”, 3^rd ed., Chapman and Hall, New York.

Childers D.G.(ed), 1978, “Modern Spectrum Analysis” IEEE Press, New York.

Ghil M. and Vautard R., 1991, “Interdecadal Oscillations and the warming trend in global temperature time series”, Nature 350 (6316), pag. 324 – 327.

Lanzerotti L.J., Thomson D.J., Meloni A., Medford L.V. and Maclennan C.G., 1986, “Electromagnetic Study of the Atlantic continental margin using a section of a transatlantic cable”, J. Geophys. Res. 91, pag. 7417-7427.

Lindberg C.R., 1986, “Multiple Taper Spectral Analysis of Terrestrial Free Oscillations”, PhD Thesis, Scripps Institution of Oceanography, University of California, San Diego.

Jenkins G.M. and Watts D.G., 1968, “Spectral Analysis and its Applications”, Holden-Day, San Francisco.

Haykin S.(ed), 1983, “Nonlinear Methods of Spectral Analysis. Topics in Applied Phisics”, 2^nd ed.,Springer-Verlag, Berlin.

Martin N., 1984, “Developpements de Mèthodes d’Analyse Spectrale Autoregressive: Application à des Signaux Rèels Non Stationnaires a n Dimension” , Thèse de docteur ingenieur, Institut Polytechnique de Grenoble, France.

Kuo C., Lindberg C. and Thomson D.J., 1990 , “Coherence established beetween atmospheric carbon dioxide and global temperature”, Nature 343, pag. 709-713.

Mann M.E., Park J. And Bradley R.S., 1995 , “Global Interdecadal and Century-scale climate oscillations durin the past five centuries”, Nature 378 , pag. 266-270.

Mann M.E., Lees J.M., 1996, “Robust estimation of background noise and signal detection in climatic time series”, Clim. Change 33, pag. 409-445.

Park J. and Maasch K.A., 1993, “Plio-pleistocene time evolution of the 100-Kyr cycle in Marine paleoclimate records”, J.Geophys. Res. 98, pag. 447-461.

Park J., Lindberg C.R. and Vernon F.L.I., 1987, “Multitaper spectral analysis of high frequency seismograms”, J.Geophys. Res. 92, pag. 12675-12684.

Pestiaux P., 1984, “Approche spectrale en modellisation paleoclimatique”, PhD Thesis, Universitè Chatolique de Louvain, Belgium.

Press W.H., Flannery B.P., Teulosky S.A. and Vettering W.T., 1988, “Numerical recipes: The art of science computing”, Cambridge University Press, Cambridge.

Rögnvaldsson O.E., 1993, “Spectral estimation using the multi taper method” Technical Report RH-13-13 Science Institute, University of Iceland, Reykjavik, Iceland.

Slepian S., 1978, “Prolate spheroidal wave functions, Fourier analysis and uncertainty – V: the discrete case”, Bell. Sys. Tech.. J. 57, pag. 1371-1430.

Thomson D.J., 1982, “Spectrum estimate and harmonic analysis”, IEEE Proc. 70(9) pag. 1055-1096.

Thomson D.J., 1990, “Quadratic-inverse spectrum estimate :applications to paleoclimatology”, Phil. Trans. R. Soc. London A 332, pag 539-597.

Yiou P., Genthon C., Jouzel J., Ghil M., Le Treut H, Barnola J.M., Lorius C. and Korotkevitch Y.N., 1991, “High-frequency paleovariability in climate and in CO₂levels from Vostok ice-core records”, J. Geophys. Res. 96(B12), pag. 20365-20378.

Yiou P., Ghil M., Jouzel J., Paillard D. and Vaultard R., 1994, “Nonlinear variability of the climatic system, from singular and power spectra of late Quaternary records”, Clim. Dun. 9, pag 371-389.

Yiou P., Baert E. and Loutre M.F., 1996, “Spectral analysis of climate data”, Surveys in Geophisics 17, pag. 619-663.

DIDASCALIE DELLE FIGURE